Quine-McCluskey minimization method uses the same theorem to produce the solution as the K-map method, namely X(Y+Y')=X

• The expression is represented in the canonical SOP form if not already in that form.
• The function is converted into numeric notation.
• The numbers are converted into binary form.
• The minterms are arranged in a column divided into groups.
• Begin with the minimization procedure.
• Each minterm of one group is compared with each minterm in the group immediately below.
• Each time a number is found in one group which is the same as a number in the group below except for one digit, the numbers pair is ticked and a new composite is created.
• This composite number has the same number of digits as the numbers in the pair except the digit different which is replaced by an "x".
• The above procedure is repeated on the second column to generate a third column.
• The next step is to identify the essential prime implicants, which can be done using a prime implicant chart.
• Where a prime implicant covers a minterm, the intersection of the corresponding row and column is marked with a cross.
• Those columns with only one cross identify the essential prime implicants. -> These prime implicants must be in the final answer.
• The single crosses on a column are circled and all the crosses on the same row are also circled, indicating that these crosses are covered by the prime implicants selected.
• Once one cross on a column is circled, all the crosses on that column can be circled since the minterm is now covered.
• If any non-essential prime implicant has all its crosses circled, the prime implicant is redundant and need not be considered further.
• Next, a selection must be made from the remaining nonessential prime implicants, by considering how the non-circled crosses can be covered best.
• One generally would take those prime implicants which cover the greatest number of crosses on their row.
• If all the crosses in one row also occur on another row which includes further crosses, then the latter is said to dominate the former and can be selected.
• The dominated prime implicant can then be deleted.

Find the minimal sum of products for the Boolean expression, f=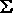(1,2,3,7,8,9,10,11,14,15), using Quine-McCluskey method.

Firstly these minterms are represented in the binary form as shown in the table below. The above binary representations are grouped into a number of sections in terms of the number of 1's as shown in the table below.

Binary representation of minterms

Group of minterms for different number of 1's

Any two numbers in these groups which differ from each other by only one variable can be chosen and combined, to get 2-cell combination, as shown in the table below.

2-Cell combinations

From the 2-cell combinations, one variable and dash in the same position can be combined to form 4-cell combinations as shown in the figure below.

4-Cell combinations

The cells (1,3) and (9,11) form the same 4-cell combination as the cells (1,9) and (3,11). The order in which the cells are placed in a combination does not have any effect. Thus the (1,3,9,11) combination could be written as (1,9,3,11).

From above 4-cell combination table, the prime implicants table can be plotted as shown in table below.

Prime Implicants Table

The columns having only one cross mark correspond to essential prime implicants. A yellow cross is used against every essential prime implicant. The prime implicants sum gives the function in its minimal SOP form.

Y = V'X + V'W + UV' + WX + UW

Copyright © 1998-2014

Deepak Kumar Tala - All rights reserved

Do you have any Comment? mail me at:deepak@asic-world.com