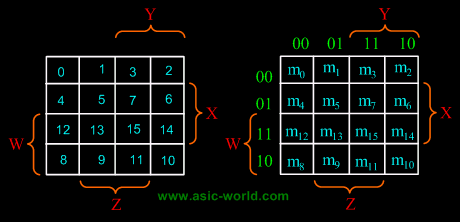
There are 16 cells in a 4-variable (W, X, Y, Z); K-map as shown in the figure below.

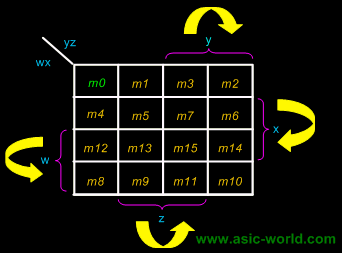
There are 2 wrap-around: a horizontal wrap-around and a vertical wrap-around. Every cell thus has 4 neighbours. For example, the cell corresponding to minterm m0 has neighbours m1, m2, m4 and m8.

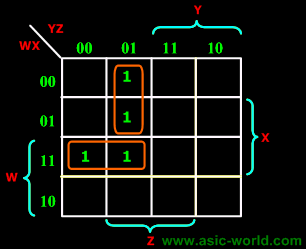
F(W,X,Y,Z) = (1,5,12,13)

F = WY'Z + W'Y'Z

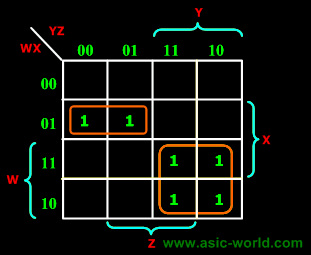
F(W,X,Y,Z) = (4, 5, 10, 11, 14, 15)

F = W'XY' + WY

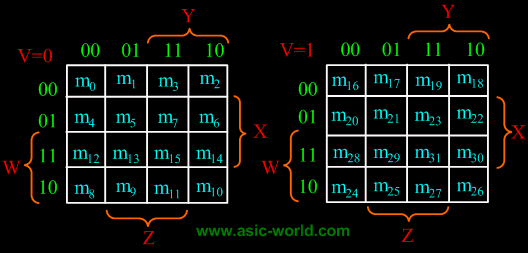
There are 32 cells in a 5-variable (V, W, X, Y, Z); K-map as shown in the figure below.

• The 0's on a K-map indicate when the function is 0.
• We can minimize the inverse function by grouping the 0's (and any suitable don't cares) instead of the 1's.
• This technique leads to an expression which is not logically equivalent to that obtained by grouping the 1's (i.e., the inverse of X != X').
• Minimizing for the inverse function may be particularly advantageous if there are many more 0's than 1's on the map.
• We can also apply De Morgan's theorem to obtain a product-of-sum expression.

Copyright © 1998-2025

Deepak Kumar Tala - All rights reserved

Do you have any Comment? mail me at:deepak@asic-world.com